백준 15489번 : 파스칼 삼각형
https://www.acmicpc.net/problem/15489
15489번: 파스칼 삼각형
첫째 줄에 양의 정수 R, C, W가 공백을 한 칸씩 두고 차례로 주어진다. (단, 2 ≤ R+W ≤ 30, 2 ≤ C+W ≤ 30, 1 ≤ W ≤ 29, C ≤ R)
www.acmicpc.net
/* 문제 설명 */
파스칼 삼각형은 양 끝을 제외한 각 수는 자신의 바로 왼쪽 위의 수와 바로 오른쪽 위의 수의 합으로 되어있다.
이때 R번째 줄, C번째 수를 위 꼭짓점으로 하는 한 변이 포함하는 수의 개수가 W인 정삼각형과 그 내부를 생각하자.
정삼각형의 변과 그 내부에 있는 수들의 합을 구하여라.

/* 해결 방안 */
현재 5번째 줄 3번째 칸에 있다면, 이는 4번째 줄 2번째 칸과 4번째 줄 3번째의 합과 같다.
자기 자신으로부터 윗 줄에서 왼쪽에 있는 애와 바로 윗 줄에 있는 애와의 합이라는 뜻이다.
따라서 점화식을 세우자면 C[r][c] = C[r-1][c-1] + C[r-1][c] 이다.
참고로, 파스칼 삼각형은 이항계수를 삼각형 모양의 기하학적 형태로 배열한 것이기 때문에 조합 공식과 같다.
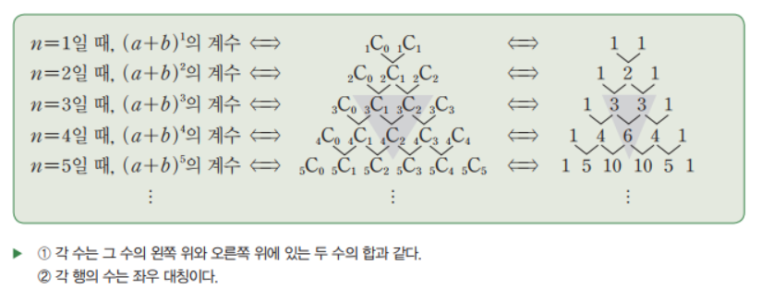
파스칼 삼각형의 맨 꼭짓점은 0C0이고, 1C0 1C1, 2C0 2C1 2C2 임을 잊지말자.
따라서 문제는 최상단 꼭짓점을 1번째 줄 1번째 원소라고 표현했는데, 이항계수(0C0)로 표현하기 위해 0번째 줄 0번째 원소라고 기준을 잡고 풀었다.
/* 구현 과정 */
1-1. for문을 돌면서 파스칼 삼각형을 만들어준다.
1-2. 점화식은 C[r][c] = C[r-1][c-1] + C[r-1][c]이다.
1-3. 처음(C[r][0])과 끝 (C[r][r])은 1이다.
2. 이 후, 따로 for문을 통해 변의 길이가 W인 정삼각형에 포함되는 값을 구해준다.
/* 소스 코드 */
#include <bits/stdc++.h>
using namespace std;
int dp[35][35], R, C, W;
int main() {
ios::sync_with_stdio(false);
cin.tie(NULL); cout.tie(NULL);
//문제에서는 R번째 줄에서 C번째 원소를 의미하지만,
//실제 파스칼 삼각형과 맞추기 위해서는 R-1, C-1이라고 생각해야한다.
//(ex, 문제에서 가장 최상단 점이 1번째 줄 1번 원소이지만
//파스칼 삼각형으로 치면 0C0로 0번째 줄 0번이라고 생각함.)
dp[0][0]=1;
for (int i = 1; i <= 30; i++)
{
//nC0, nCn은 둘 다 1이다.
dp[i][0] = 1; dp[i][i] = 1;
for (int j = 1; j < i; j++)
dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];
}
cin >> R >> C >> W;
long long ans = 0;
for (int i = 0; i < W; i++)
for (int j = 0; j < i + 1; j++) {
ans += dp[R - 1 + i][C - 1 + j];
}
cout << ans;
}
/* 얻어갈 점 */
1. 이항계수의 합 공식을 떠올리기 어려울 때는 파스칼 삼각형을 생각하자.
2. 내 위에 있는 애 중 왼쪽에 있는 애랑, 내 위에 있는 애를 합친 것
3. C[r][c] = C[r-1][c-1] + C[r-1][c]
'Algorithm > BOJ' 카테고리의 다른 글
| [백준 1756] 피자 굽기 (0) | 2021.04.10 |
|---|---|
| [백준 18238] ZOAC 2 (0) | 2021.04.03 |
| [백준 9440] 숫자 더하기 (2) | 2021.03.28 |
| [백준 14939] 불 끄기 (1) | 2021.03.25 |
| [백준 17609] 회문 (0) | 2021.03.21 |